Fu Nxn
N→∞ Z1 0 xnf(x)dx = 0 3 Let P∞ n=0 ane −nx be a series which converges at x = 0 Prove that the series converges uniformly on the interval 1,∞) 4 Let {fn(x)} be a sequence of continuous functions on 0,∞) Show that the set E of points x for which {fn(x)} converges is Borel measurable 5 Let {ak} be a sequence such that the.

Fu nxn. N = liminf X n} Or argue directly) If this event has probability 1 we say {X n} converges almost surely, or X n → X as (In this case the limit X is a random variable because it equals the limsup) 23 Distributions Most important questions about X are “what values does it take on, with what probabilities”?. And r2» µ(xn;Y0n) = gµ(Ynjxn) Z fµ(xnjxn¡1) n rloggµ(Ynjxn)rlog fµ(xnjxn¡1)2 r2 logg µ(Ynjxn)r 2 log f µ(xnjxn¡1) £pµ(xn¡1jY0n¡1)dxn¡1 2gµ(Ynjxn) Z fµ(xnjxn¡1)rloggµ(Ynjxn) rlog fµ(xnjxn¡1)rpµ(xn¡1jY0n¡1) dxn¡1 gµ(Ynjxn) Z fµ(xnjxn¡1) r 2p µ(xn¡1jY0n¡1) dxn¡1 (11) Except in some simple cases, no closedform expression can be obtained for either. Haiyu Huang on any interval containing 0 or with 0 as an endpoint It suffices to show f does not converge uniformly on (0,†) and (¡†,0)First observe that f is unbounded f µ 1 m2 X1 n˘1 1 1¯n2/m2 m n˘1 1 1¯(n/m)2m n˘1 1.
Where A = σ2/n τ2σ2/n = 0107 B = τ2 τ 2σ /n =3 n = 27 σ = 9 τ = √ 25 = 5 θ = 70, and x = 71 Hence µ ∼ N(7169,268), so that graphically, the prior and posterior distributions are. N B Then for each µ× νmeasurable set C ∈ C the section xC is measurable for almost all x, the function fC(x) = ν(xC) is Ameasurable, and (µ× ν)(C) = Z X fC(x)dµ(x) (62) Proof Note that (X×Y,A N B,µ× ν) must be σfinite as well, so that X×Y = n∈N × Yn where µ()ν(Yn). Nondifferentiable optimization by smoothing for nondifferentiable f that cannot be handled by proximal gradient method • replace f with differentiable approximation fµ (parametrized by µ) • minimize fµ by (fast) gradient method complexity #iterations for (fast) gradient method depends on Lµ/ǫµ • Lµ is Lipschitz constant of ∇fµ • ǫµ is accuracy with which the smooth.
N N f sum w weight = = = Σ= = Sample mean Population mean () Weighted mean Mean for frequency table highest value lowest value Midrange 2 x x n x N wx x w f x x f µ ∑ = ∑ = ∑• = ∑ ∑• = ∑ = 2 2 2 2 Range = Highest value Lowest value Sample standard deviation 1 Population standard deviation Sample variance Population. F(µ)f(µ0)sin(°)d›d›0 Thus flnal free energy will be F = F0 kBT(ln(n) Z f(µ)ln(4f(µ))d›L2Dn Z Z f(µ)f(µ0)sin(°)d›d›0 (211) This is a functional and it’s hard to get an exact function which minimizes it We will approximate a trial function with a parameter and get a parameter to minimize it With a trial function3,. 1 c(N) c(N !.
Gauss’ theorem 3 This result is precisely what is called Gauss’ theorem in R2The integrand in the integral over R is a special function associated with a vector fleld in R2, and goes by the name the divergence of F divF = @F1 @x @F2 @y Again we can use the symbolic \del" vector. Yingwei Wang Real Analysis Choosing ε = 1 n, then we can get a sequence (zn) ∞ =1 satisfying limn→∞ d(x,zn) = 0 According to Section 32, x ∈ E¯ “⇐” If x ∈ E¯, by the previously Section 32, there is a sequence (zn)∞ n=1 in E such that limn→∞ d(zn,x) = 0 Then d(x,E) = infz∈E d(x,z) = limn→∞ d(zn,x) = 0 42. Base from which the limit theorems related to can be systematically derived To deflne geometric moment contraction, let X0 0 » be independent of X0 » and (µk)k‚1 and deflne (x) = Fµn – Fµn¡1 – – Fµ1(x) Thus (X 0 0) can be viewed as a coupled version of (X0) We say that is geometricmoment contracting.
(2) where , Yn, and Zn are the tristimulus values of the reference white, L∗. Defining gn(x) = 1 x n ¢n e¡2x for 0 • x • n 0 for n < x we have an increasing sequence of nonnegative Lebesgue measurable functions The limit function is g(x) = exe¡2x = e¡x for all x ‚ 0 having used part (a) So by Lebesgue’s Monotonic Convergence Theorem we find that. N=¡1 cne 2inµ=L So the Fourier series are part of the class of trigonometric series Deflnition 28 A trigonometric polynomial is a trigonometric series of period L with flnitely many terms In other words, XN n=¡N cne 2inµ=L 23 Some Convergence Results There are some natural questions regarding the Fourier series of a function f as.
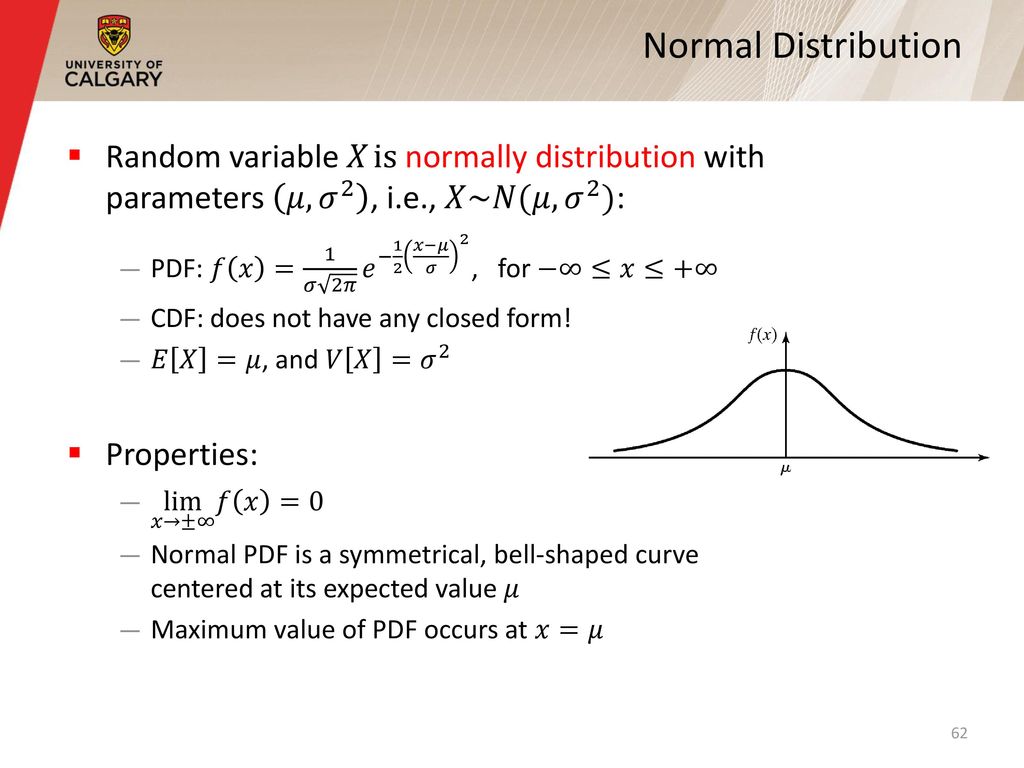
Distributions Derived from Normal Random Variables χ 2 , t, and F Distributions Statistics from Normal Samples Normal Distribution Definition A Normal / Gaussian random variable X ∼ N(µ, σ. If {E i} ∞ i=1 is a sequence of disjoint µ ∗measurable sets, set F S n = n i=1 E i and F= ∞ i=1 E iThen for any A, µ∗(A∩F n) = µ ∗(A∩F n∩E n)µ ∗(A∩F n∩E C n) = µ ∗(A∩E n)µ(A∩F n−1) Iterating this shows that µ∗(A∩F n) = i=1 µ∗(A∩E j) From the µ ∗measurability of F n and the subadditivity of µ, µ∗(A) = µ∗(A∩F n)µ ∗(A∩FC n. F µ Y Yn ¶ − 16 116 ¸ a∗ = 500 · f µ X ¶ −f µ Y Yn ¶¸ b∗ = 0 · f µ Y Yn ¶ −f µ Z Zn ¶¸ f(w) = w1/3 if w > 7787w 16 116 otherwise C∗ ab = (a ∗2 b∗2)1/2 hab = tan−1 à b∗ a∗!.
Find the Derivative f(x)=1/(x^n) Apply basic rules of exponents Tap for more steps Rewrite as Multiply the exponents in Tap for more steps Apply the power rule and multiply exponents, Move to the left of Rewrite as Differentiate using the Power Rule which states that is where. By Taylor approximation, we have E h e s σ √ n (Xk−µ) i = E 1 s σ √ n (Xk −µ) s2 σ2n (Xk −µ)2 O( 1 σ3 √ n3 (Xk −µ)3) = (1 0 s2 2n) Therefore, MZn(s) = 10 s2 2n n (a) −−→ es 2 2, as n → ∞ To prove (a), we let yn = (1 s 2. 2 f µ t $ t k =0 k & 2 L 2 f µ (t 1) tf(x t) " f t 1 •quadratic convergence attains εaccuracy within O(loglog 1 ε) iterations •typically requires storing and inverting Hessian ∇2f(x) ∈Rn×n •a single iteration may last forever;.
• Interpreted as messages passed from node x N to node x 1 ψ (x ,x )ψ (x x )ψ (x ,x ) Z p(x) 1,2 1 2 2,3 2, 3 N 1,N N 1 N 1 = − − The image cannot be displayed Your computer may not have enough memory to open the image, or the image may have been corrupted Restart your computer, and then open the file again. K→∞ X n k (ω) = X(ω) for every ω ∈ AC The next application of BorelCantelli lemma shows that LP(Ω,F,µ) is complete Definition 7 (Cauchy sequence) Let E be a metric space with metric d A sequence {x n}∞ n=1 in E is a Cauchy sequence if, for every # > 0 there exists N such that d(x n,x m) < # for all m,n ≥ N. SAMPLE EXAM QUESTION 2 SOLUTION (a) Suppose that X(1) < < X(n) are the order statistics from a random sample of size n from a distribution FX with continuous density fX on RSuppose 0 < p1 < p2 < 1, and denote the quantiles of FX corresponding to p1 and p2 by xp1 and xp2 respectively Regarding xp1 and xp2 as unknown parameters, natural estimators of these quantities are X(dnp.
Classification (Contd) • As we can see, to classify a point we have to evaluate an Ndimensional integral, where N is the size of the training set. 1 The Standard Dozen Throughout this lecture, we refer to convex and concave functions Write I and I0 for the intervals a;b and (a;b) respectivelyA function f is said to be convex on I if and only if ‚f(x) (1 ¡ ‚)f(y) ‚ f(‚x (1 ¡ ‚)y) for all x;y 2 I and 0 • ‚ • 1 Conversely, if the inequality always holds in the opposite direction, the function is said to be concave. 1) Parking Spaces Stage 1 Stage 2 Stage 3 StageNN!.
¯X !n,´93 $ \ ¯X !nF2X ¾X g ¯X ÄX ¼X g ¯X ÄX Ë,´ = Ñ Ä5 0 = Ñ Å È v ¾ ) AÞ 7,´,´ = ÑL F Ä(© Ê !n F4Ö Ê 7F2X ¾ ¯X Ë = Ñ ¼ ÄX Ë5 X g,´ ¦ N© Ä = Ñ4Ö Ê Å ÄB 1y = Ñ4Ö Ê 7L¿Lt ¾F2X,´ = Ñ È F65 7 >F2X,´ = Ñ 0 6Ci)· ¼ = Ñ 7 ú ' > L ¶ 7F2X ¾ \ ¯X !n. N=−∞ f(xn) is integrable, then f= 0 ae Problem 10 Suppose f is integrable on R nand for a fixed h∈ R let g(x) = f(x h) be a translate of f Show that gis also integrable and that R R n gdx= R R fdx Problem 11 Let (X,F,µ) be a finite measure space, and f a nonnegative realvalued function defined on X Prove that a necessary and. Prohibitive storage requirement QuasiNewton methods 132.
1) kk1 Heuristic Cost Heuristic ÒFutureÓ System x k1 = f k(x k,u k,w k) x k Observations Belief Statep k Controller µ k Control u k = µ k(p k) QFactors Current State x k x0 x1 x k xN x " N x "" N u k u. The asymptotic distribution of µ^ m;n in (4) is a convolution of two independent normal distributions The proof of this is not simple, however, for three reasons First, the flnite sample terms from which these arise (the two terms on the right in. .
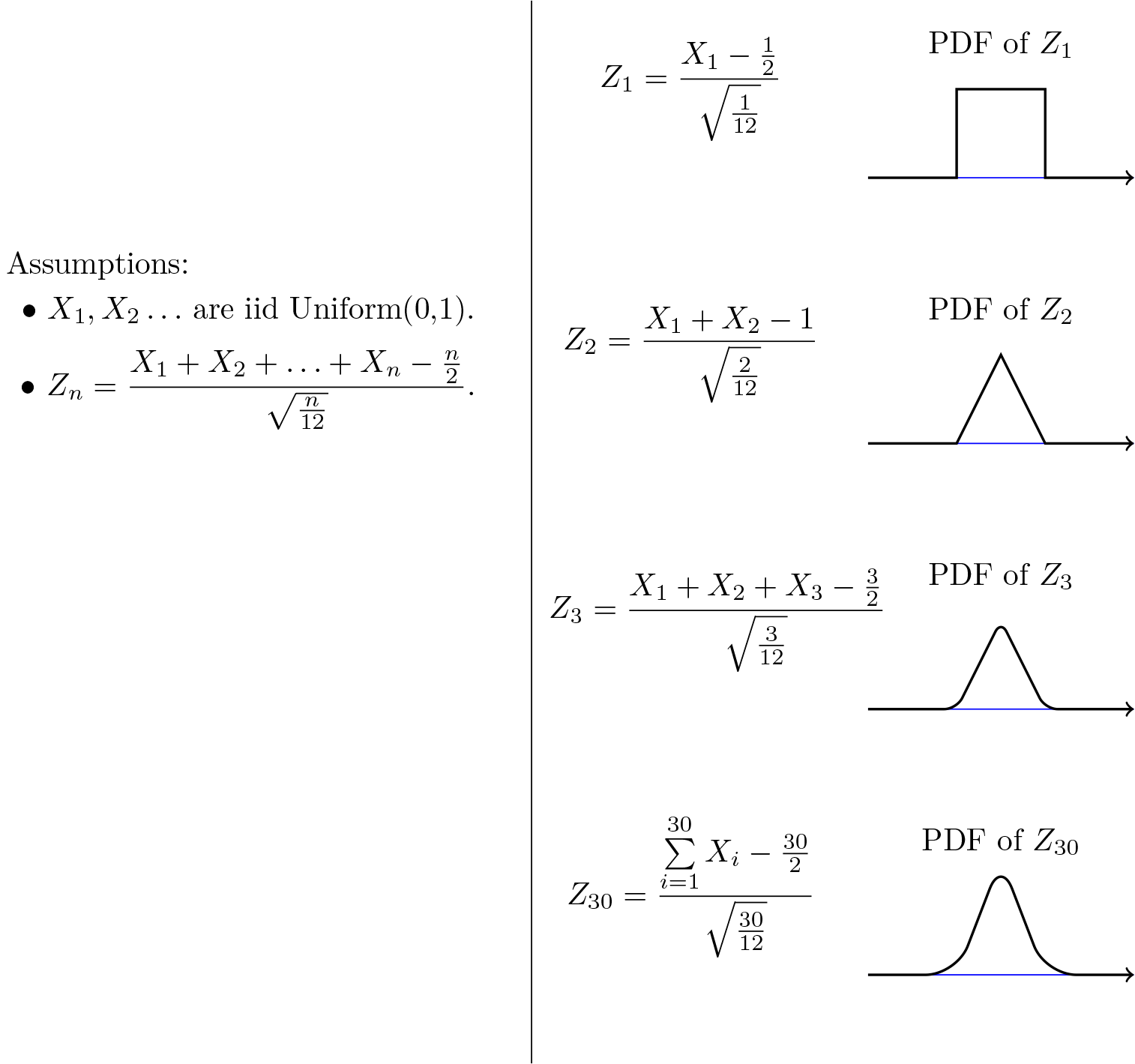
(X n t n) F 1 F 1 F µ 0 (t 1) F µ 0 (t n) Since the X’s are now continuous rv, the substitution of CDFs with pdf’s yields q n (t 1, ,t n)= f µ 1 (t 1) f 1 (t n) f µ 0 (t 1)f µ 0 (t n) In the specific case where device “lives” (X) are exponentially distributed, this becomes q n (t 1, ,t n)= 1 µ 1 exp(t 1 µ) 1 µ exp(t n. 1 (6 points) Multiple choice (each is 1 point) Please flnd the best possible answer from the following problems and mark your answer Let X1;¢¢¢; be iid sample Let fµ(x) and Fµ(x) be the common PDF and CDF respectively Let µ^ be the MLE of µ, µ0 be the true parameter, L(µ) be the likelihood function, ‘(µ) be the loglikelihood function, and I(µ) be the Fisher information matrix. 2 1 INTRODUCTION Let {}∞n=1 denote iid random variables, all taking values in RDefine Sn= X1 ··· ∀n ≥1 Recall the classical centrallimittheorem Theorem11(CLT) If EX1=µand Var(X1)=σ2 ∈(0,∞),then Sn −nµ p n ⇒N(0,σ2), where ⇒ means weak convergence (or convergence in distribution), and N(m,v) denotes the normal distribution with mean m ∈ R and variance.
Example 72 If N is equipped with counting measure, then Lp(N) consists of all sequences fx n 2R n2Ngsuch that X1 n=1 jx njp. Claim frequency Let N denote the number of claims in the period Aggregate loss We denote the amount of the ith claim by Xi and the aggregate loss by S,sothat S = X1 X2 ···XN Claim severity The average claim severity is the sample mean of {Xi}, ie, X¯ = S/N Pure premium Let E be the number of exposure units of the risk. Prove that the norm k·kX is induced by a scalar product, and thus X is a Hilbert space Show that {xn}∞ n=1 must then be an orthonormal sequence Solution We denote by S the linear span of {xn}∞ n=1 (the set of finite linear combinations of elements in {xn}∞ n=1)By property (b), we find that on S the norm k· kX coincides with the ℓ2norm of its coefficients.
Nonsmooth optimization minimize x∈Rn f(x) where fis convex but not always differentiable •subgradient methods yield εaccuracy in O 1 ε2 iterations •in contrast, if fis smooth, then accelerated GD yields εaccuracy in O 1 √ ε iterations —. Algebra for Lemma 6 of “Competition Policy as Strategic Trade”¤ Marc Rysman July 11, 01 Let ¯ x = xP 0=P0 and ¯ y = yP 0=P0 Note that the condition that QP 0=P0 is constant implies that ¯ x and ¯ y are constant In this notation, the optimal. In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomialAccording to the theorem, it is possible to expand the polynomial (x y) n into a sum involving terms of the form ax b y c, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positive.
F µ (n−k) g and γ(n) h = k=0 n k Suppose that X n is asymptotically normal. Now we will show that Σ is closed under countable unions By Problem 24, it suffices to show that Σ is closed under countable disjoint unions. An approximation to ln(µ) with fµ;.
25 Outer Measures 55 Thus, µ∗ is finitely additive on Σ However, µ∗ need not be finitely additive on arbitrary subsets of X!. B) such that x 0 = a, x N = b and ¶ (x n) = ¶ (a) n N (¶ (b) µ ¶ (a));. X0 f(x0) = inff= lim k fn k (xn k) 6 The conditions that Wald (1949) imposed to get consistency of the MLE imply epiconvergence of Kn to K(when there are no missing data and no Monte Carlo) If fhas a unique minimizer x, then xis the only cluster point of the sequence.
In o²ine learning, we have a batch of data x1n = fx1;x2;;xng We typically optimize cost functions of the form f(µ) = f(µ;x1n) = 1 n i=1 f(µ;xi) The corresponding gradient is g(µ) = rµf(µ) = 1 n i=1 rµf(µ;xi) For linear regression with training data fxi;yign i=1, we have have the quadratic cost f(µ) = f(µ;X;y) = (y¡ Xµ)T. Derivative examples Example #1 f (x) = x 3 5x 2 x8 f ' (x) = 3x 2 2⋅5x10 = 3x 2 10x1 Example #2 f (x) = sin(3x 2) When applying the chain rule f ' (x) = cos(3x 2) ⋅ 3x 2' = cos(3x 2) ⋅ 6x Second derivative test When the first derivative of a function is zero at point x 0 f '(x 0) = 0 Then the second derivative at point x 0, f''(x 0), can indicate the type of that point. 1 ´ n ´ N µ 1 Since ¶ is nondecreasing we have x n ± 1 < x n for all 1 ´ n ´ N, and it follows that P = f a = x 0 < x 1 < < x N = b g.
Posterior of µ ∼ N A×θ B ×x, τ 2σ nτ 2σ!. ;X n ˘F The goal is to estimator the mean of the underlying distribution µ 0 =E(X 1)= R xdF(x) The MoM estimator works as follows Assume that the sample size n = KB, where K is the number of subsamples and B is the size of each subsample We first randomly split. Let N ¶ 2 be a positive integer Since ¶ is continuous we can use the intermediate value theorem to °nd points x n 2 (a;.
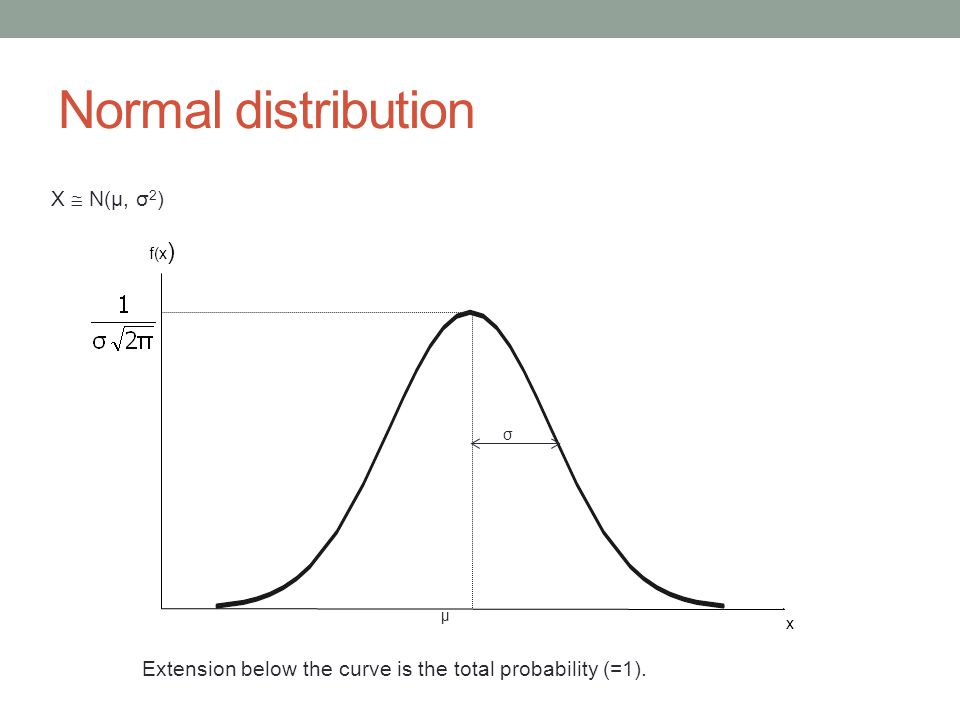
• The notation N(µ, σ2) means normally distributed with mean µ and variance σ2 If we say X ∼ N(µ, σ2) we mean that X is distributed N(µ, σ2) • About 2/3 of all cases fall within one standard deviation of the mean, that is P(µ σ ≤ X ≤ µ σ) = 66. N be an enumeration of rational numbers in R (a) Show that R\∪∞ n=1 (r n− 1 n2,r n 1 n2) is never empty (b) Show that R\∪∞ n=1 (r n− 1 n,r n 1 n) can be empty or nonempty, depending on how the rationals are enumerated (a) By the σsubadditivity of the Lebesgue measure m ∪∞ n=1 (r n− 1 n 2,r n n2) ≤ X∞ n=1 m (r n. N(x) = x/n This sequence converges pointwise to the zero function on R Example 3 Consider the sequence {f n} of functions defined by f n(x) = nxx2 n2 for all x in R Show that {f n} converges pointwise Solution For every real number x, we have lim n→∞.
Initial State 15 1 5 18 4 19 9 21 25 8 12 13c(0) c(k) c(k 1) c(N !.
Normal Distribution Ppt Video Online Download
Inhomogeneous Levy Processes In Lie Groups And Homogeneous Spaces Springerlink

Xfitter 2 0 0 Heavy Quark Matching Scales Unifying The Ffns And Vfns Cern Document Server
Fu Nxn のギャラリー

Catena Poly Aquacopper Ii Bis M N N Bis Pyridin 4 Yl Isophthalamide Aquacopper Ii Di M Sulfato Dimethylformamide Disolvate Topic Of Research Paper In Chemical Sciences Download Scholarly Article Pdf And Read For Free On Cyberleninka Open

New Page 1
The Surprisingly Cool Physics Of Pushing A Block Against A Wall Wired

Chapter 5 Slutsky S Theorem 10 Fundamental Theorems For Econometrics

Solved Let X N M S2 Be A Normal Random Variable Define Chegg Com
Central Limit Theorem
Lois Normales Maths Cours

Solutions To Statistical Infeence By George Casella

Chapter 5 Slutsky S Theorem 10 Fundamental Theorems For Econometrics

X Follows Normal Distribution N M S2 With Pdf F And Cdf F If Max F Homeworklib
Osa Primary Aberrations Of A Thin Lens With Different Object And Image Space Media
Mathsv Affichage Des Cours En Ligne

Lecture 13 Martingales Pdf Free Download

Answered Suppose X1 X2 Are Independent Bartleby
A Uniform Ladder Of Length L Rests Against A Smooth Vertical Wall
4 Simulation Of Random Variables Foundations Of Statistics With R

Solved 8 Let X1 X2 Be A Random Sample Of Si Chegg Com
Newton S Laws Of Motion

Performance Of Ls Svm C 0 2 C 1 C 2 1 2 G 1 Gaussian Download Scientific Diagram

One Million Values Were Simulated From X N µ S 2 N For µ 2 And Download Scientific Diagram

The Density Function F For The Parameters N 2 µ 3 S 1 And Download Scientific Diagram

Cadlag Stochasticities Levy Processes Part 1 Altexploit

Prove That Int Vert Vert F N Vert Vert F N F Vert P Vert F Vert Vert D Mu To 0 If Sup N Vert F N Vert Leq C Mathematics Stack Exchange

Let F N In L P X Mathbb X Mu 1 Leq P Infty And Let Beta N Defined For E In Mathbb X By Mathematics Stack Exchange
Plos One Spatio Temporal Characteristics Of Global Warming In The Tibetan Plateau During The Last 50 Years Based On A Generalised Temperature Zone Elevation Model

Solved 5 Let X N M S2 Be A Normal Random Variable De Chegg Com

Lecture4 Pdf Mathematical Analysis Measure Theory

Mobius Inversion Formula Wikipedia

Normal Force And Friction Force Ck 12 Foundation
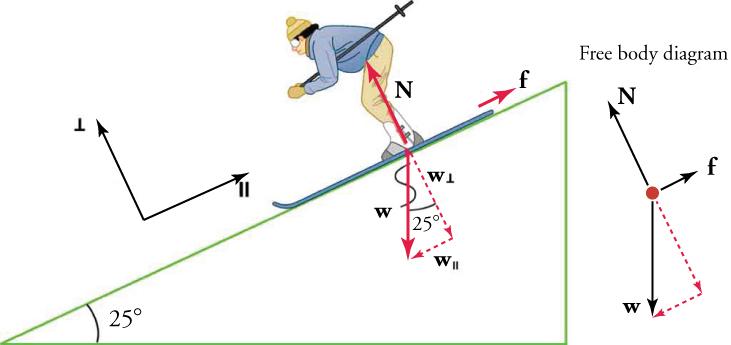
5 4 Inclined Planes Texas Gateway

8 Mg 0 5 Mx 0 4 7 Kg F U 0 35 Kg If A Force F Of 100 N Is Applied To Block Of Mass 7 Kg Then Acceleration Of 35 Kg Mass Will Be 1 2 4 Ms 2 2 1 Ms 2 8 Ms 2 3 0 4 Ms 2

Theory Of Probability Statistics For Business And Economics
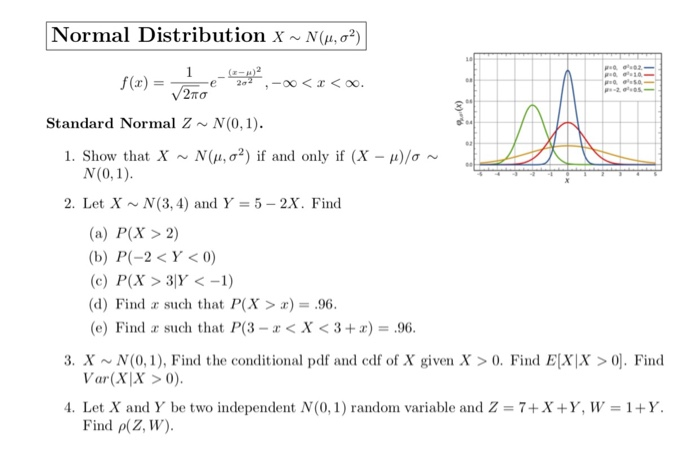
Solved Normal Distribution X N M S2 F X V2ps E 2 Chegg Com

Key Formulas Chapter 2 Mean For Ungrouped Data µ X N And
Bayesian Optimization For Materials Design Deepai

Normal Distribution Wikipedia
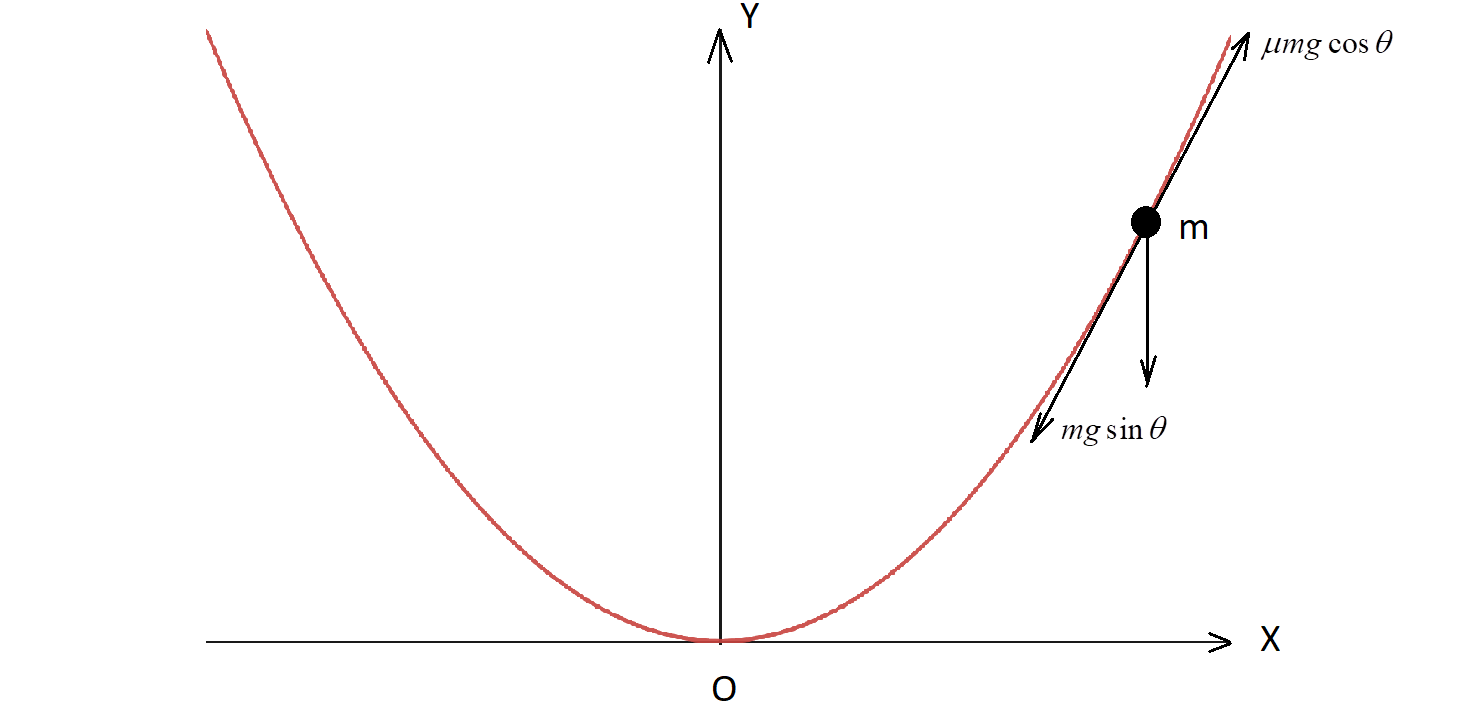
A Bead Of Mass M Is Located On A Parabolic Wire With Class 11 Physics Jee Main

Values Of X N Y N And F N From 9800 To 10 000 Under F For M E Download Scientific Diagram
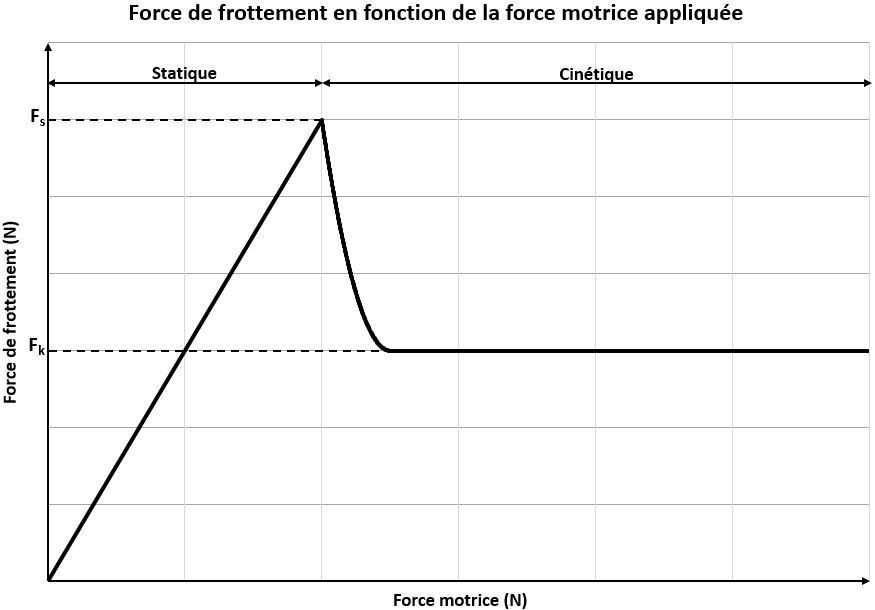
La Force De Frottement Alloprof

Ppt H Tim M Th F Bna Xo Q F Bn Sp Hna Nmc Wªp C N Im S N Kvt L Tama P Sylx 2 Powerpoint Presentation Id

Integration Et Probabilites Td1 Espaces Mesures Corrige Pdf Telechargement Gratuit

Numerically Statistical Simulation Of The Intensity Field Of The Radiation Transmitted Through A Random Medium

Friction

Physics Page In Mathematics A Gaussian Function Often Simply Referred To As A Gaussian Is A Function Of The Form F X E X B 2 2c 2 For Arbitrary Real Constants A B And

Chapter 4

The Absolute Value Of D F 2 N µ N X Dx For N 1 2 3 And 4 In Download Scientific Diagram

Mobius Function Wikipedia
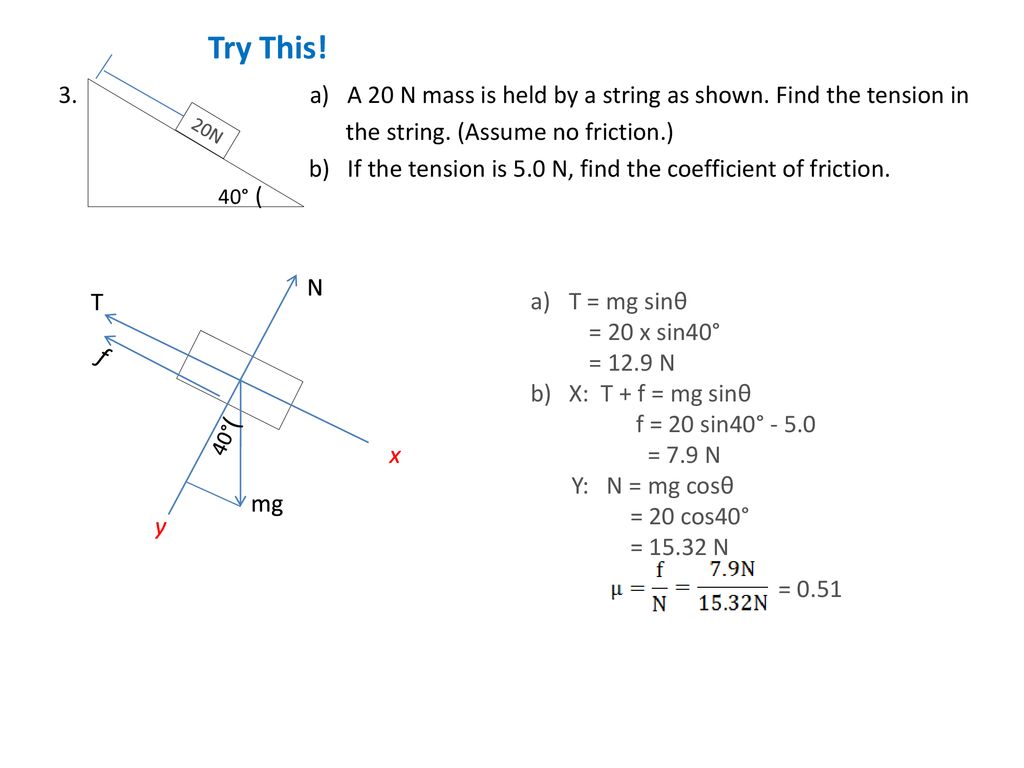
Unit 5 Equilibrium Lesson 2 Friction Ppt Download
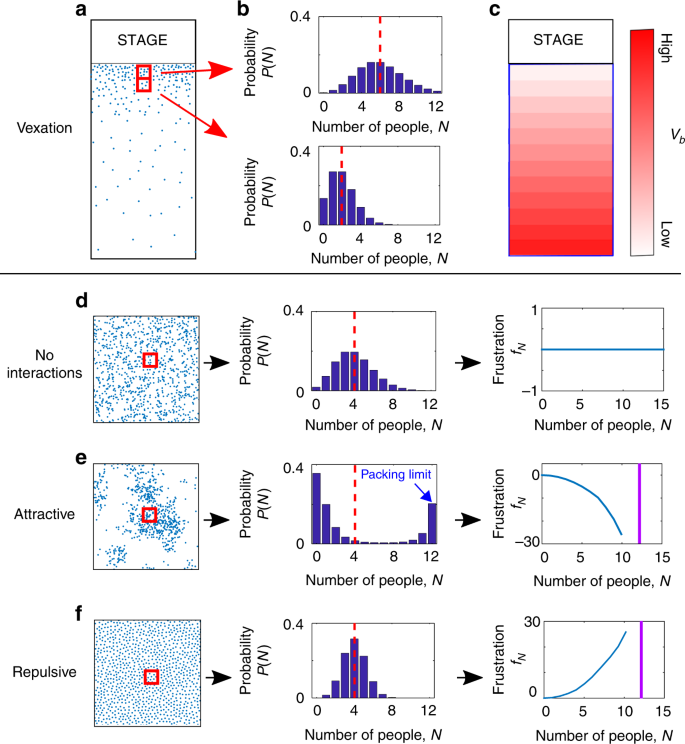
Density Functional Fluctuation Theory Of Crowds Nature Communications
Bayesian Optimization With Expensive Integrands Deepai

Language Recurcif

Answered Practice 2 Given µ Find U When X Bartleby

Maximum Likelihood Estimation Explained Normal Distribution By Marissa Eppes Towards Data Science
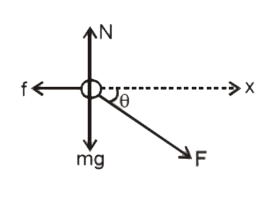
A Block Having A Mass 3kg Is Initially At Rest On A Horizontal Su

Statistical Inference Part Iv Location And Scale Parameters

5 Manieres De Calculer La Force Normale Wikihow

Gnuplot Demo Script Prob Dem
If A Block Of Mass M Is Kept On A Horizontal Surface With Friction Coefficient Math Mu Math Then What Would Be The Minimum Force Needed To Move That Block On The Surface
Osa Primary Aberrations Of A Thin Lens With Different Object And Image Space Media

Tinkutara Equation Editor Math Forum Question
Cpsc 531 System Modeling And Simulation Ppt Download

Mathematics 539 Exercises 2 Dirichlet Series And Euler Products µ

Solved Let X1 Denote A Random Sample From A N Chegg Com

Data Analysis And Data Mining 2 Programmer Sought

Cours De Probabilites A Saint Louis Senegal Rhodes Remi Pdf Telechargement Gratuit

Synthesis Structure Electrochemistry And Magnetic Properties Of Face Sharing Bioctahedral Nickel Complexes Containing A N3ni M S2 M X Nin3 Core X F Cl Br N3 Oh Sciencedirect

The Number Of Monomials In N In H F The Number Of The Divisors Download Scientific Diagram

Show That There Is F In L 1 X Mu With P F Infty And P F N F To 0 As N To Infty Mathematics Stack Exchange
Osa Primary Aberrations Of A Thin Lens With Different Object And Image Space Media

Why Int X 2g D Mu Le Liminf N To Infty Int X Bigl 2g F N F Bigr D Mu Mathematics Stack Exchange

Univariate Tests Stests

Riemann Zeta Function Wikipedia

Friction

Ppt Forces Newton S Laws Powerpoint Presentation Free Download Id
Questions On Convergence Of Explicit Formulas For F X Sum Limits N 1 X A N Where A N In Left Mu N Right Mu N Phi N Lambda N Mathematics Stack Exchange

Table 1 From Bis M N N Di 3 Pyridyl 2 6 Pyridine 2 6 Dicarboxamide K2 N N Bis Dibromidomercury Ii N N Dimethylformamide Disolvate Semantic Scholar
Maximum Likelihood Estimation Of Gaussian Parameters

Dea1 Estimation Method For Determining Frequency And Phase Shift In A Data Transmission Network Whereby An Estimation Algorithm Is Derived From A Suitable Cost Function Determined From A Likelihood Function In
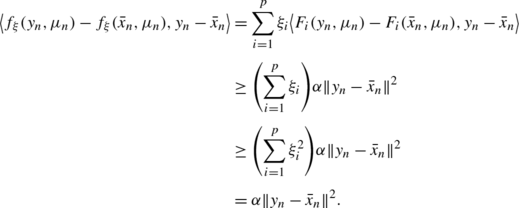
Semicontinuity Results On Parametric Vector Variational Inequalities With Polyhedral Constraint Sets Springerlink

Multiplicative Number Theory I Classical Theory Cambridge

5 Manieres De Calculer La Force Normale Wikihow
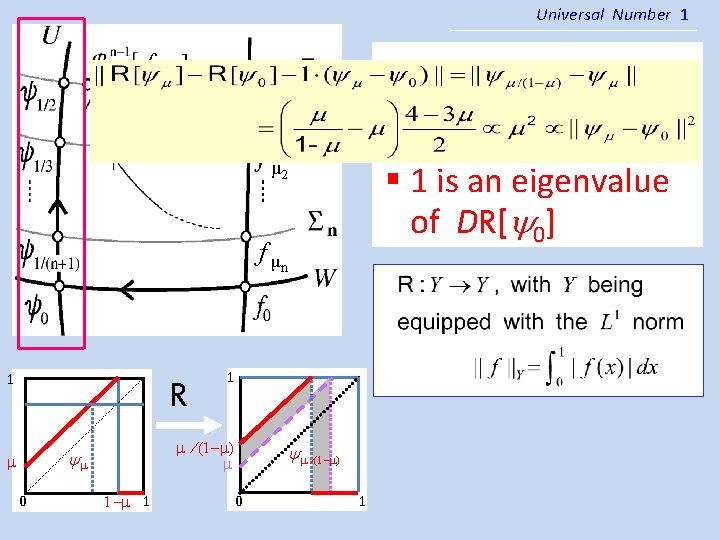
Bo Deng Outline Department Of Mathematics Small Chaos

Translating N µ S 2 Random Variables Problem Suppose X N µ

Gnuplot Demo Script Prob Dem

Su Jin Kim Gyeongsang National University Fall Ppt Download

117 A Body Of Mass 100 G Is Sliding From An Inclined Plane Of Inclination 30 What Is The Frictional Force Experienced If U 1 7 1 1 7x12x Tn 2 1 7x 13 Xzn 3 1 7 X 13 N 4 1 7 X 12 Xan

Solved 3 Let X N M S2 Be A Normal Random Variable Def Chegg Com

Riemann Zeta Function Wikipedia

Kg 630 N 57 U03bc 7 6 M S 2 What Is The Magnitude Of The Normal Force The Ceiling Course Hero

Fatou S Lemma Wikipedia
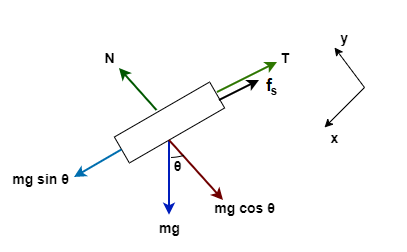
A N Crate Is Held At Rest On An Incline Clutch Prep




